Imbalanced examples in object detection

这周看了一篇《Learning a Unified Sample Weighting Network for Object Detection》.分析的是Imbalance between positive and negative examples.由此，找了其余的一些cvpr2020paper以及这里的经典methods.

Introduction:

• sampling strategy: 对于one stage， 一次生成目标区域和目标分类，要求在进行proposal采样时，规则(regular)和稠密(dense)的进行采样，带来一个突出的问题：background即负样本的数量会远远高于foreground即正样本的数目，带来了二者之间的不平衡。
  而对于two stage，proposal采样的过程是在第一阶段如RPN网络中进行的，是一种稀疏(sparse)的采样方式。
  这里的稀疏和稠密，是相对于classification而言的, 二阶段算法对classification而言，foreground和background之间的比例更合理一些，稀疏采样带来的结果是foreground在所有proposal中更稠密；一阶段算法密集采样则是foreground在proposal中更稀疏。
• metrics 最常用的metric：mAP
  首先定义几个相关的值，TP/FP/TN/FN:T=True，表示检测正确；F=False，表示检测错误；P=Positive，表示检测结果为阳性(GT=True)；N=Negative，表示结果为阴性(GT=False)；
  具体到object detection中，TP的含义就是正确地检测到了阳性，可以理解为检测成功的部分；FP的含义是错误地检测到了阳性，即假阳性，检测结果Iou<threshold或者同一个GT的多个检测框被淘汰部分；FN的含义是错误地检测到了阴性，即GT存在但是未检出；TN正确检测到了阴性，无意义。
  精确率(Average Precision)：$AP=\frac {TP}{TP+FP}= \frac {TP}{all \space predictions}$
  召回率(Average Recall): $AR=\frac{TP}{TP+FN}=\frac{TP}{all \space ground truth}$
  在不同IOU(Iou=0.5/0.75/0/9)下，对不同的class计算AP(AR)，求得在不同Iou下的所有class的平均AP(AR),称为mAP(mAR).

Focal Loss in RetinaNet

FAIR Kaiming he组，ICCV 2017 best student paper

• Background: 由于dense exampling中positive和negative的极不平衡，传统的CE Loss会导致网络在训练过程中positive在训练过程中被稀释。我们将一些检测结果不好(通常其loss值都会比较高)称为hard examples，在这里，hard example被假设为最需要关注的examples.
  已有了一些OHEM(Online Hard Examples Mining)等方法处理hard example.

• Methods:

  • 最核心的改变是focal loss，思路是人工改变网络对不同样本分布的attention.
    顺着这个思路：Hard examples是最需要关注的样本-> Hard examples 普遍是比较难以分类的example->hard example 普遍loss高(score 低)-> 设计loss function时考虑提高loss高(score 低)的example的weight.

    • FL loss Equation:
      $FL(p_{t})=-\alpha_{t}(1-p_{t})^{\gamma}log(p_{t}))$
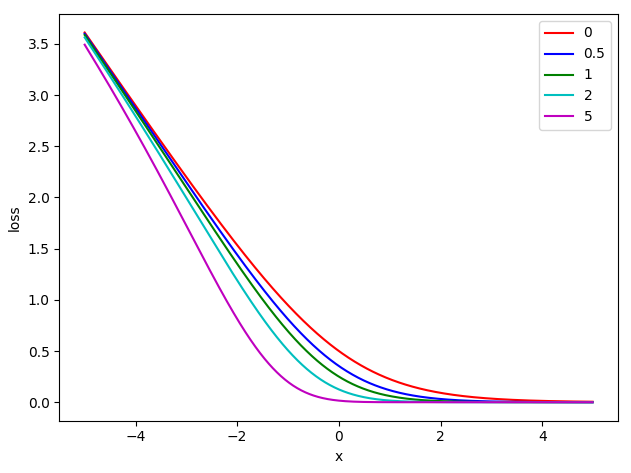
      $\alpha_{t}$和$\gamma$为Hyper Parameters，显然，当$\gamma>1$，$p_{t}$越低，$log(p_{t})$前的权重值越高；因此，focal loss提高了hard example在训练过程中的权重.

      以下为$\alpha_{t}=0.5$，不同$\gamma$值的loss随$x_{t}$变化的图像：

      

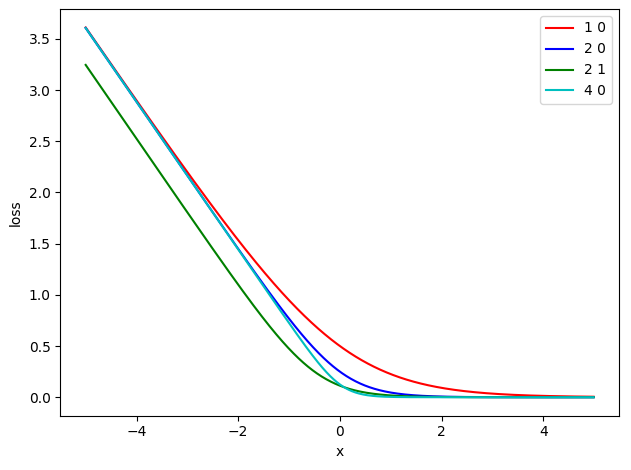
      • FL* loss Equation: $FL* = -\alpha_{t}log(\sigma(\gamma x_{t}+\beta))/ \gamma$

        其中$\gamma$和$\beta$为Hyper Parameters ，以下为$\alpha_{t}=0.5$，不同$\gamma$、$\beta$值的loss随$x_{t}$变化的图像：

        

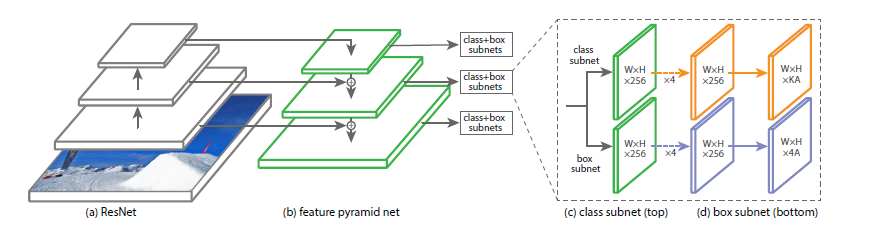
    • 网络结构：

• Questions:

  • Why hard example effects?

  

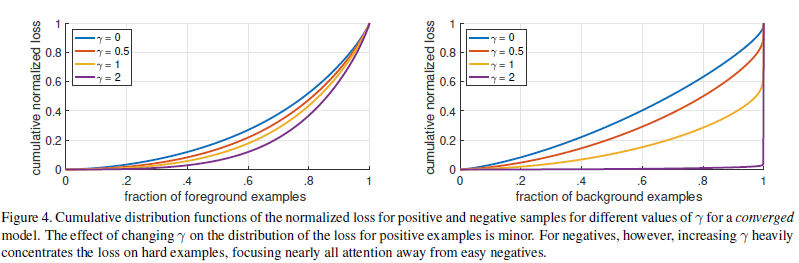
  From this Figure, $\gamma$越高，说明hard example权重越高。图为positive(negative) example按升序排列的accumulatIve normalized loss(归一化累计loss)，可以看出，positive examples中，最难的20%样例的loss在总loss中比重随$\gamma$值增大而增大，negative examples中，现象更加显著。说明，focal loss确实完成了想法。

  • greater $\gamma$, better performance? 按照实验结果来看，$\gamma=5.0$比较$\gamma=2.0$，mAP掉了1.8%，显然并不是$\gamma$越高结果越好；我认为合理的解释是，$\gamma$升高到2后，Easy Example的权重就会处于相对较低的水平；再升高$\gamma$，降低的是中等confidence的example，而这些样例对performance可能有着不可忽视的影响。Hard example更需要注意这个假设过于宽泛，这也是很需要改进的。

• Appendix：

  顺手记录一下loss函数导数的推导吧：
  \(\begin{aligned} p_{t} &= \frac{e^{x_{t}}}{\sum{e^{k}}} = \frac{1}{1+e^{-x}} (softmax和sigmoid导数相同)\\ CE(p_{t}) &= -ylog(p_{t}) \\ FL(p_{t}) &= -(1-p_{t})^{\gamma}log(p_{t}) \\ \frac{dp_{t}}{dx} &= \frac{e^{x}\sum{e^{k}}-e^{x}e^{x}}{(\sum{e^{k}})^{2}} \\ &=\frac{e^{x}}{\sum{e^{k}}}\frac{\sum{e^{k}}-e^{x}}{\sum{e^{k}}}=p_{t}(1-p_{t}) \\ \frac{dCE}{dx} &= \frac{dCE}{dp_{t}} \times \frac{dp_{t}}{dx} \\ &=y \times \frac{1}{p_{t}} \times p_{t} \times (1-p_{t}) = y(p_{t}-1)\\ \frac{dFL}{dx} &=y[\gamma (1-p_{t})^{\gamma -1}logp_{t}-(1-p_{t})^{\gamma}\frac{1}{p_{t}}] \times p_{t}(1-p_{t})\\ &=y[\gamma(1-p_{t})^{\gamma}p_{t}log(p_{t})-(1-p_{t})^{\gamma+1}] \\ &=y(1-p_{t}^{\gamma})(\gamma p_{t}log(p_{t})+p_{t}-1) \end{aligned}\)

Other Paper in CVPR2020

• Learning from noisy anchors for one stage object detection:

key: 利用定义的值cleanliness来描述candidate proposal，通过localization accuracy和classification confidence的加权平均来计算；
通过这个cleanliness来动态调整不同candidate proposal在训练中的权重

• Unified Sample Weighting Network

key: not only ‘hard’ example matters, but ‘easy’ one. jointly re-weights classification and regression loss.

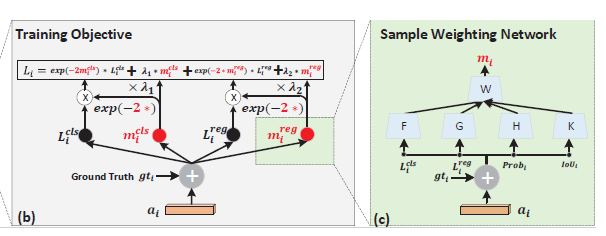
$m_{i}^{reg}$和$m_{i}^{cls}$利用高斯分布推出，并进行正则化

• Prime Sample Attention in Object Detection

key: ‘hard’ examples are not as import as ‘IOU-highest’ positive samples or ‘score-highest’ negative samples. Sort IOU and Scores in hierarchy and adjust weights dynamicly.

• Equalization Loss for Long-tailed Object Recognition

  imbalance between positive and negative can be seen as long-tailed distribution which negative sampels are nearly 90% long-tail, rare.

key: reducing rare category’s negative samples from easy category(positive samples in easy category will be regarded as negative in rare)

The same position with $(1-p_{t})^{\gamma}$ in focal loss, $w_{j}=1-E(r)T_{\lambda}(f_{j})(1-y_{i})$,；对$E(r)=1$，表示r是foreground类别，0则表示background；$T_{\lambda}(f_{j})=1$表示类别为rare，0表示为easy；$1-y_{j}=1$表示对当前类别为负样本negative，0表示positive； 因此，$W_{J}=0$表示，这个proposal被分为rare类别的负样本，也就是之前提到的easy类别的正样本，需要将这部分negative训练时产生的影响去除。