Convolution and Transposed
This is a exhaustive paper for different kind of convolution computation, but the arithmetic is not enough.
The paper: https://arxiv.org/abs/1603.07285
The Github(including gifs):https://github.com/vdumoulin/conv_arithmetic
Introduction
-
convolution: strides: 步长; padding:0填充; kernel: 卷积核尺寸; padding中的特例: 1、half padding: if $k=2n+1$, then when $p=n=[k/2]$, it’s called half padding; 2、full padding: if $p=k-1$ and $s=1$, it’s called full padding.
-
pooling: 可以理解为特殊kernel的卷积
在pytorch中,torch.nn.Maxpooling()有一个参数为ceil_mode,当ceil_mode为True时,将会向上取整
eg: input=5, kernel=2, strides=2, padding=0,
if ceil_mode=True, output=3; else, output=2
-
transposed convolution: 卷积的一种,虽然称为反卷积(UpSampling), 核心操作仍然是卷积
Relationship of conv and it’s trans
We define $i$ as input size, $o$ as output size, $k$ as kernel size, $s$ as stride size, $p$ as padding size, and $x^{‘}$ ($x={i,o,p,k,s}$) as transposed operation parameters.
$o=i^{‘}$ $i=o^{‘}$ $k^{‘}=k$ is obvious.
$o=\frac{i-k+2p}{s}+1$ is also obvious, its called Equation1.
$o^{‘}=\frac{i^{‘}-k^{‘}+2p{‘}}{s^{‘}}+1$ called Equation2.
When $s^{‘}=s=1$, We will get $p^{‘}=k-p-1$;
And when $s>1$, to get a solution, we set the $i^{‘}_{new}=o+(o-1) \times m$, which $m$ cells will be inserted into every cell in original feature map. Like photo below.
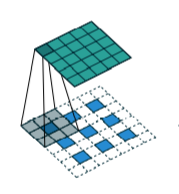
After simplification, there will be:
$(1+m)\frac{s^{‘}}{s}=1$, called Equation 3;
$(1+m)(\frac{2p-k}{s}+1)-m-k+2p^{‘}+s^{‘}=0$,called Equation 4.
We will get:
$m=\frac{s}{s^{‘}}-1$ and $2p-k+s^{‘}-ks^{‘}+2p^{‘}s^{‘}+s^{‘2}=0$.
Obviously, 2 equations and 3 paras, let s=$s^{‘}=1$, a viable solution is $m=s-1 \space p^{‘}=k-p-1$. That’s enough.